Setiap distribusi tentu memiliki parameter statistik tertentu. Jika data tidak normal penyajian data menggunakan median dan minimum maksimum sebagai pasangan ukuran pemusatan dan penyebaran.
Cara Mengatasi Data Berdistribusi Tidak Normal Semesta
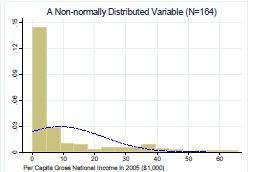
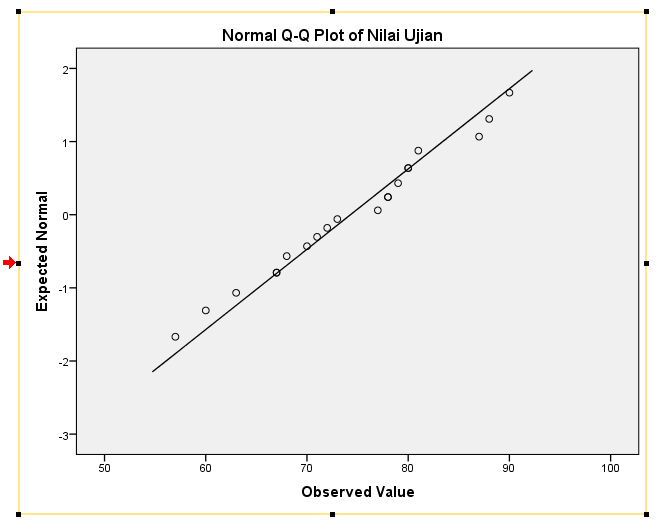
Contoh data tidak normal. Ya 1 dan tidak 0. Angka tidak bermakna matematika. Dalam hal ini asumsi normalitas jelas tidak dapat terpenuhi nilai p kurang dari 005 dan lebih dari 5 persen dari titik data berada di luar interval kepercayaan 95 persen. Seorang peneliti telah mengumpulkan data yang akan diolah dengan program spss. Apabila luasnya sawah yang di lampung 100000 hektare ha dan produktivitas padi berdistribusi normal data tentatif tentukan berikut ini. Probabilitas plot pada gambar di atas adalah contoh dari uji normalitas.
Oleh karena itu sebelum melakukan analisis statistik parametrik terlebih dahulu kita harus melihat apakah data kita terdistribusi normal atau tidak. Hitam 1 abu abu 2 putih 2. Pengalaman saat melihat distribusi data yang tidak normal adalah banyaknya data dengan nilai yang sama sementara data dengan nilai lain tidak mengikuti contohnya seperti ini. Namun untuk memberikan kepastian data yang dimiliki berdistribusi normal atau tidak sebaiknya digunakan uji normalitas. 70 siswa mendapatkan nilai 90. Untuk uji hipotesis gunakan uji non parametrik.
Rata rata produktivitas padi di lampung tahun 2009 adalah 6 ton per hektare ha dengan simpangan baku s 09 ton. Cara mengatasi data berdistribusi tidak normal ketika kita hendak melakukan analisis statistik parametrik seperti melakukan uji korelasi product moment salah satu asumsi yang harus dipenuhi adalah distribusi data kita normal. 2 siswa nilai 81. Data tentang hasil belajar siswa yang berjumlah 100 siswa dengan rentang nilai 0 100 didapatkan. Kedua parameter ini akan digunakan untuk menggenerate data yang lainnya. Sedangkan pada variabel prestasi memiliki nilai kolmogorov smirnov sebesar 0105 dan p0027 p005 dengan demikian.
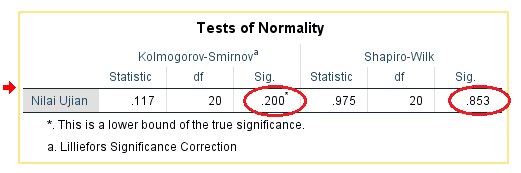
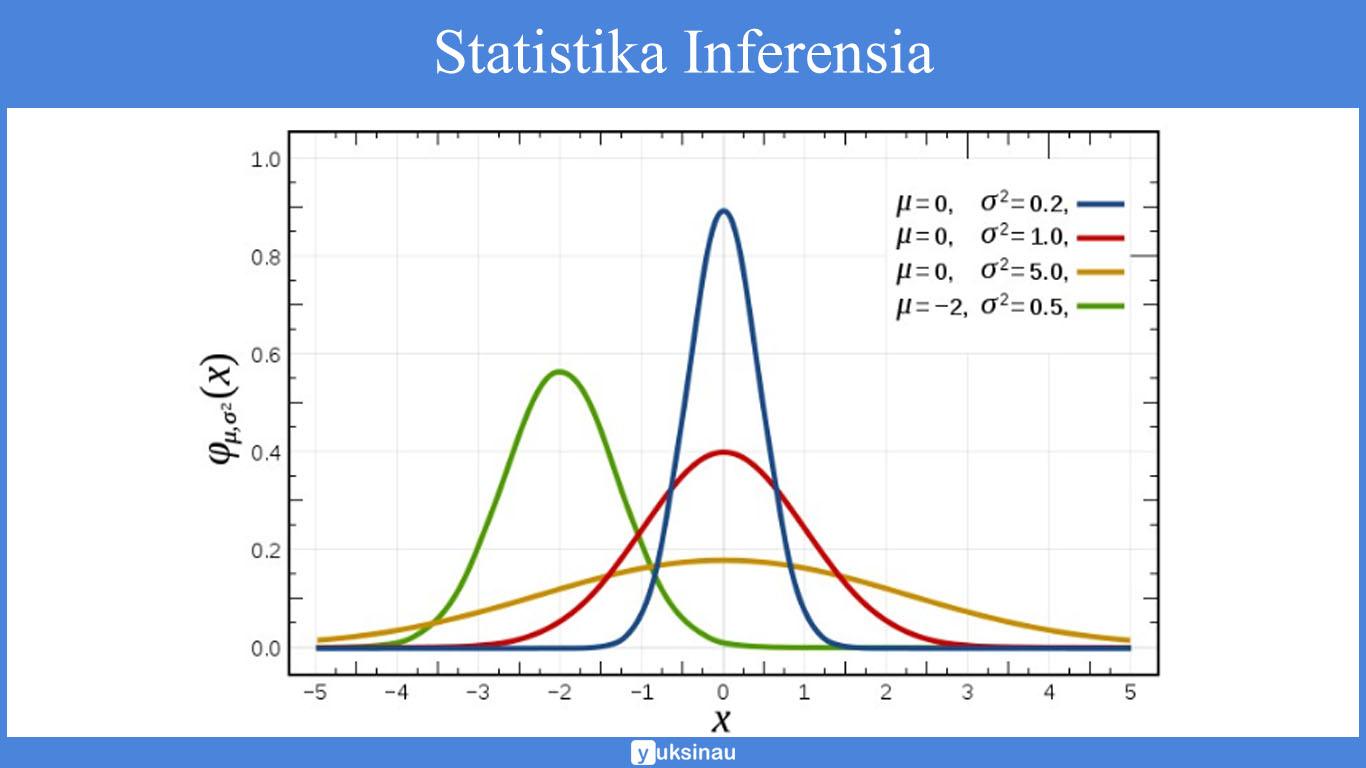
Running data berdasarkan asumsi. Dari output tersebut dapat kita lihat variabel iq memiliki nilai kolmogorov smirnov sebesar 053 dan p0200 p005 dengan demikian tidak ada perbedaan antara distribusi empirik data kita dengan distribusi normal ideal oleh karena itu distribusi data variabel iq normal. Pria 1 dan wanita 0. Sebagai contoh jika kita mengasumsikan data berdistribusi normal maka minimal kita harus mengetahui dua parameter yaitu mean dan standar deviasi. Maka sesuai dengan dasar pengambilan keputusan dalam uji normalitas kolmogorov smirnov di atas dapat disimpulkan bahwa data berdistribusi normal. Tidak memiliki efek evaluatif karena hanya menempatkan angka ke dalam kategori tanpa struktur tidak memiliki peringkat dan tidak ada jarak.
Interpretasi uji normalitas kolmogorov smirnov dengan spss berdasarkan tabel output spss tersebut diketahui bahwa nilai signifikansi asiympsig 2 tailed sebesar 0993 lebih besar dari 005. 3 siswa nilai 83. Skala ini menempatkan angka sebagai atribut objek. Uji statistik normalitas yang dapat digunakan diantaranya chi. Karena belum tentu data yang lebih dari 30 bisa dipastikan berdistribusi normal demikian sebaliknya data yang banyaknya kurang dari 30 belum tentu tidak berdistribusi normal untuk itu perlu suatu pembuktian.