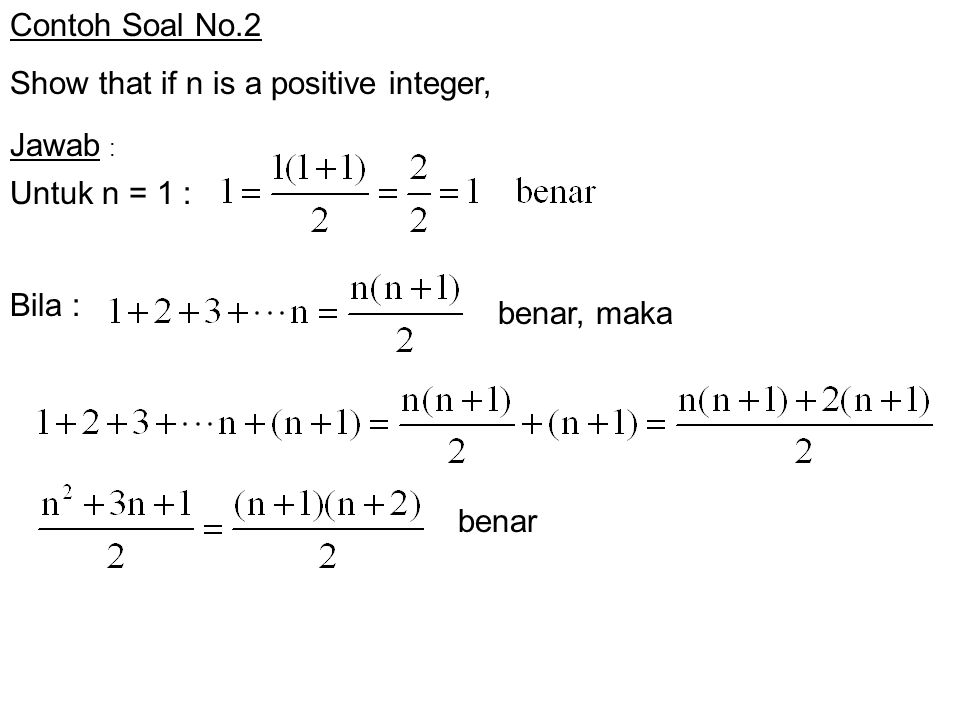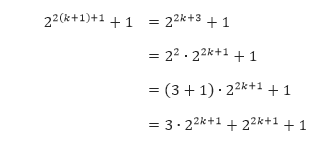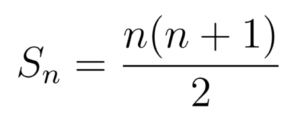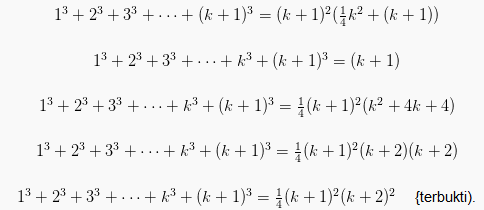Pertama kita harus menunjukkan bahwa rumus tersebut benar ketika n 1. Kumpulan soal mudah sedang sukar.
Contoh Soal Dan Pembahasan Induksi Matematika Sederhana Youtube
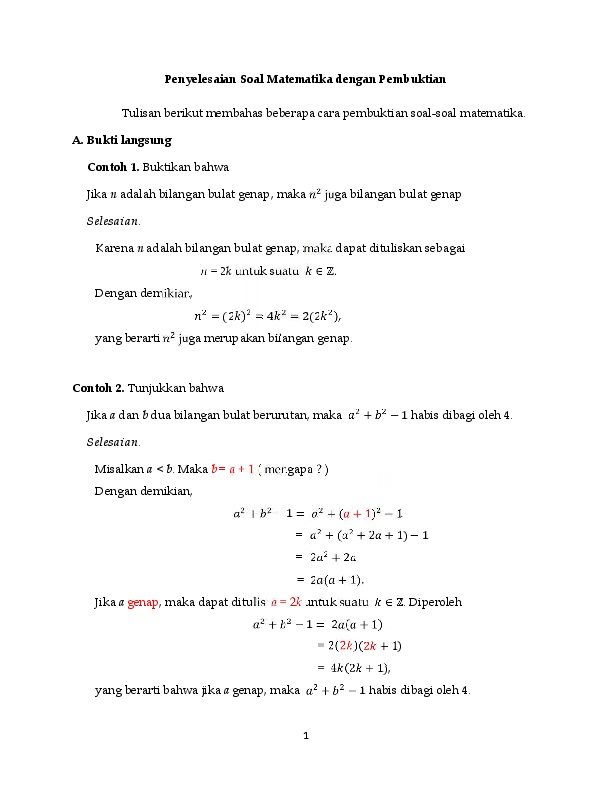
Contoh soal induksi matematika sederhana. Induksi matematika materi yang membahas tentang pengertian materi pembahasan dan contoh soal induksi matematika secara lengkap dan terperinci. Jangan lupa untuk perbanyak latihan soal. Pembahasan induksi matematika terdiri dari dua bagian yang berbeda. Buktikan bahwa 2n n 20 untuk setiap bilangan bulat n 5. Itu singkatan dari quod erat demonstrandum. 6 n 4 habis dibagi 5 untuk n bilangan asli.
Di sini kamu akan belajar tentang induksi matematika melalui video yang dibawakan oleh bapak anton wardaya. Soal induksi matematika kelas 12 kurikulum 2013 qed. Kamu akan diajak untuk memahami materi hingga metode menyelesaikan soal. Untuk semua bilangan bulat n 1. I basis induksi. Jika kalian ingin memahaminya dengan jelas silahkan kalian simak materinya dibawah ini gaes.
Guru sd smp sma contoh soal induksi matematika sederhana. Contoh soal induksi matematika 3. Untuk n 5 kita peroleh 25 5 20 adalah suatu pernyataan yang benar. Misalkan bahwa 2k k 20 adalah benar. Ii langkah induksi. Contoh contoh soal induksi matematika 1.
Gunakan induksi matematika untuk membuktikan rumus untuk semua bilangan bulat n 1. Pembahasan induksi matematika terdiri dari dua bagian yang berbeda. Berikut ini adalah beberapa contoh dari pernyataan matematika yang bisa dibuktikan kebenarannya pada induksi matematika. 2 4 6 2n nn 1 n bilangan asli pn. Contoh file soal uts lengkap kelas 1 6 sdmi semua mata pelajaran 20162017 berikut ini adalah kumpulan dari berbagi sumber tentang contoh soal induksi matematika sederhana yang bisa gunakan untuk bank soaldownloadsd dan diunduh secara gratis dengan menekan tombol download biru dibawah ini. Soal induksi matematika kelas 11 kurikulum 2013 revisi.
Gunakan induksi matematika untuk membuktikan rumus. Induksi matematika merupakan materi yang menjadi perluasan dari logika matematikalogika matematika sendiri mempelajari pernyataan yang bisa bernilai benar atau salah ekivalen atau ingkaran sebuah pernyataan dan juga berisi penarikan kesimpulan. Induksi matematika tidak bisa dipakai untuk menurunkan atau menemukan rumus. Sekarang kita peroleh 2k1 22k 2k 20 2k 40 k 1 20 iii konklusi. Maka disimpulkan bahwa. Ketika n 1 rumus tersebut benar karena.
Pertama kita harus menunjukkan bahwa rumus tersebut benar ketika n 1ketika n 1 rumus tersebut benar karena bagian kedua induksi matematika memiliki dua langkah.
Gallery of Contoh Soal Induksi Matematika Sederhana
